Area-Velocity
The area-velocity method consists of knowing the hydraulic area (A) by dimensional means and the speed (V) by means of a meter, either digital or analog, and applying the Castelli equation (Q=AV) to know the flow rate (Q). To do this, and following the NMX-179, the area and speeds must be discretized into a number of segments according to the width of the channel.
Area-Velocity in channels
Area-Velocity in Pressure Pipe
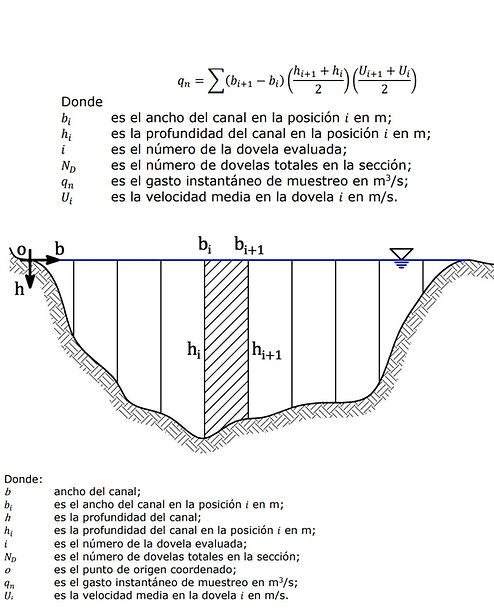
Area-Speed by Mean-Section Voussoirs
Water flow measurement is a constant requirement in multiple fields of engineering, from water resource management to the operation of industrial systems, treatment plants, distribution networks, and metrology laboratories.
Among the various methods available, one of the most widely used due to its simplicity and versatility is the Area-Velocity method, which allows flow rate to be calculated based on two fundamental variables: the area through which the fluid flows and its velocity.
This method can be applied to both closed pipes and free-surface channels, although each method presents important specificities regarding flow behavior and the parameters that must be considered for an accurate measurement.
Basic Principle of the Area-Velocity Method
The basic principle behind the method is quite intuitive: to know how much water is passing through a point, it is enough to know the size of the space through which it flows (the area) and the velocity at which it moves. Multiplying these two quantities gives the volumetric flow rate.
However, in practice, this calculation poses several challenges. For example, water velocity is not uniform throughout the section; it is typically faster in the center and slower at the walls or bottom, if the flow profile has already developed, due to friction. Therefore, it is important to refer to the mean velocity, which can be estimated with various instruments depending on the case, such as electromagnetic flowmeters, ultrasonic sensors, etc.
When flow occurs inside a closed pipe, the behavior of water is influenced by its velocity, viscosity, and pipe size. This is where a parameter called the Reynolds number comes into play, which is used to classify the type of flow: whether it is smooth and orderly (laminar) or turbulent and chaotic.
However, this is not what most influences the correct flow measurement. In the real world, when talking about water flow in a closed pipe, the Reynolds number will be in the tens or hundreds of thousands, so it will be turbulent in almost all scenarios. What the Reynolds number can help us with is correcting the velocity profile, which determines the velocities at different points within the pipe's cross-section.
If you'd like to learn more about the topic, check out our other article:
When flow occurs in open channels, such as rivers, ditches, or irrigation canals, the situation changes. Here, the dominant influence is gravity, as water flows along gradients rather than pressure, as in the previous case.
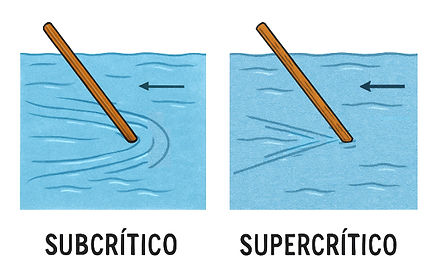
In this context, the Froude number becomes the key parameter. This number compares the velocity of the water with the speed at which waves propagate on the surface. If the water moves slowly, waves can travel in both directions (subcritical flow), but if it moves very quickly, waves cannot return (supercritical flow). This distinction is vital, as it affects the shape of the flow and, therefore, the strategy for measuring it correctly.
Castelli's Contribution and Bernoulli's Legacy
The origin of the Area-Velocity method dates back to the dawn of modern hydraulics. In the 17th century, the Italian Giovanni Benedetto Castelli, a disciple of Galileo Galilei, was one of the first to study the movement of water from an experimental perspective. He observed that the flow rate of water exiting an orifice depended on both the size of the orifice and the height of the water above it.
Although his studies were still empirical, they marked a turning point. His work influenced Daniel Bernoulli, who, decades later, would develop the famous principle that bears his name, which describes how energy is conserved in a moving fluid.
Where:
Q: flow rate (volume per unit time)
A: cross-sectional area
V: mean flow velocity
In this article, we offer three calculators that will suit your needs: one for pipe flow and two for free surface flow. In the latter case, there are two methods. One is obtained through the hydraulic area of a lined channel, typically rectangular or trapezoidal, by calculating the cross-sectional area and entering the velocity. In the second, we offer the mean-section method, which discretizes the flow into segments or sections to determine the velocity and depth of the channel at each point. This is done with the goal of obtaining a more accurate profile of the average axial velocity in the channel.
At Axotek, we listen to our users. If you need a calculator to make your work and/or projects easier, you can contact us, and as soon as possible, we'll have it online at no cost to you.
.png)
