Pressure Unit Converter
The Enigma of Pressure: An Essay on Its Nature, Measurement, and Applications in the Modern World
Pressure, that seemingly simple concept we learn in our first physics lessons, is in fact a phenomenon of profound implications that permeates every aspect of our universe, from the blood flow in our veins to the titanic forces that shape the stars. Here, he explores the multidimensional nature of pressure, not as a mere abstract concept, but as a bridge between scientific theory and the practical applications that define our technological civilization.
In its most basic form, pressure is defined as the force applied per unit area, a description that, while accurate, barely scratches the surface of its complexity. To understand its true meaning, we must consider its role as a mediator between the microscopic and the macroscopic. In a gas, for example, pressure emerges from molecular chaos: millions of particles colliding against the walls of their container generate a distributed force that we perceive as pressure. This kinetic model, developed by luminaries such as James Clerk Maxwell and Ludwig Boltzmann, reveals that pressure is not a static entity, but rather the statistical manifestation of a frenetic molecular ballet.
Pressure can be expressed and used in so many ways that how it is interpreted depends on your needs:
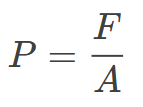
Where:
-
F = Applied force (in Newtons, N)
-
A = Area over which the force acts (in square meters, m²)
Example: If you exert a force of 50 N on a surface area of 2 m², the pressure will be 25 Pascals (Pa).
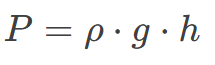
Where:
-
P = Pressure at a depth hh (in Pa)
-
ρ = Density of the fluid (in kg/m³)
-
g = Acceleration due to local gravity ≈ 9.81 m/s²
-
h = Depth from the surface (in meters)
Example:
-
Determine the pressure at the bottom of a water tank, lake, or submarine.
-
Example: In water (ρ = 1000 kg/m³), at a depth of 5 m:
P = 1000 x 9.81 x 5 = 49.050 Pa (≈49 kPa).
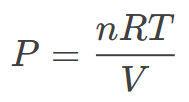
Where:
-
P = Gas pressure (in Pa)
-
n = Amount of substance (moles)
-
R = Universal gas constant (8.314 J/mol K)
-
T = Absolute temperature (in Kelvin)
-
V = Volume of the container (in m³)
Example:
-
Calculate the pressure in a balloon, tire, or closed gas system.
-
Example: A balloon with 0.5 moles of gas at 300 K and 0.02 m³:
P = 0.5 x 8.314 x 3000.02 = 62.355 Pa (≈62.4 kPa).
These formulas reveal how pressure adapts to different environments, from solids to fluids and gases.
If pressure is universal, its measurement is marked by a Tower of Babel of units that reflects humanity's cultural and technical diversity. The Pascal (Pa), a unit of the International System, honors the polymath Blaise Pascal, but competes with the Anglo-Saxon psi, the industrial bar, the medical mmHg, and the atm of chemistry textbooks. This proliferation is not a mere historical whim, but the result of practical adaptations: tires are measured in psi because the first pressure gauges emerged in industrial England; doctors prefer mmHg because of its connection to mercury in traditional sphygmomanometers.
The coexistence of these units poses an epistemological challenge: how to communicate critical values—such as the pressure of a nuclear reactor or that of a scuba tank—unambiguously? This is where the importance of conversion tools, which act as translators between technical languages, emerges.
An error in units can have catastrophic consequences, as in the famous case of the Mars Climate Orbiter, lost in 1999 due to a conflict between measurements in newtons and pounds-force.
The domestication of pressure is a common thread in the history of technology. Watt's steam engines harnessed steam pressure to power the Industrial Revolution; automobile hydraulic brakes multiply the force of the driver's foot thanks to Pascal's principle. In medicine, blood pressure—that 120/80 mmHg number we eagerly consult in the doctor's office—is a thermometer of cardiovascular health, while in astronomy, radiation pressure explains how solar winds sculpt the tails of comets.
But pressure is also a double-edged sword. In the deep ocean, pressure crushes submarines not designed to withstand it; in a diver's lungs, it can trigger decompression sickness if not managed precisely. Even in everyday life, "social" or work pressure metaphorizes how this physical concept infiltrates our language to describe intangible tensions.
Studying pressure is, ultimately, studying relationships: between force and space, between science and culture, between innovation and risk. In a world that depends on increasingly complex systems—from gas pipeline networks to space travel—understanding and accurately measuring pressure is not an academic luxury, but a vital necessity. Tools like unit converters, far from being mere technical utilities, are symbols of a collective effort to standardize knowledge and avoid the misunderstood silences that can lead to disaster.
So, the next time we adjust our tire pressure or measure our blood pressure, we are participating in a modern ritual that links fundamental physics with human experience: a reminder that, in a universe governed by invisible forces, precise measurement is our antidote to chaos.
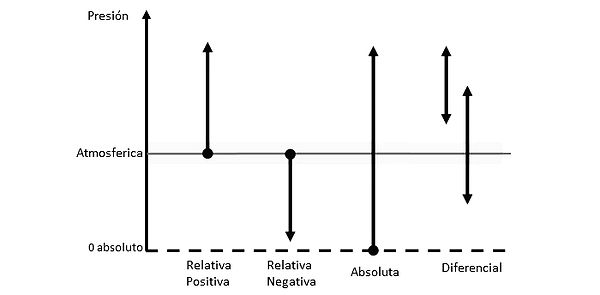
Now, within the study of pressure, we can also find a subdivision of pressures, which depend on their reference and direction, these are:
- Positive Relative Pressure (gauge): Atmospheric pressure is used as a reference, and pressure is added to the system from there.
- Negative Relative Pressure (vacuum): Atmospheric pressure is used as a reference, and pressure is removed from it.
- Absolute Pressure (barometric): Absolute vacuum or absolute zero pressure is used as a reference, and pressure is added from there.
- Differential Pressure (DP): This is the difference between two pressures with the same reference, usually relative.
.png)