Flow Unit Converter

The concept of flow is fundamental to disciplines ranging from physics and engineering to biology and economics. It represents the transfer or movement of a physical quantity (such as mass, energy, particles, or information) through a medium or system in a given time. Its study has led to technological advances, improvements in industrial processes, and a deeper understanding of natural phenomena.

Volumetric flow (or rate) is a fundamental quantity in engineering and applied sciences. It quantifies the volume of a fluid (liquid or gas) that passes through a cross-section (usually a pipe or channel section) per unit of time. Understanding it is critical for designing pumping systems, distribution networks, industrial equipment, and even for modeling natural phenomena such as blood flow or ocean currents.

Volumetric flow (Q) is defined as:

Where:

Q: Flow rate (m³/s).
V: Volume of fluid (m³).
t: Time (s).
v: Average fluid velocity (m/s).
A: Cross-sectional area of the pipe or conduit (m²).

The second equality, also known as the continuity equation or Castelli equation, establishes a direct relationship between fluid velocity and conduit cross-sectional area. However, this apparent simplicity hides an underlying complexity when we consider factors such as viscosity, density, turbulence, profile, and compressibility of fluids. For gases or liquid hydrocarbons and petroleum products, the situation is more complex due to their compressible nature, requiring the use of thermodynamic equations that consider changes in density and temperature.

Accurate volumetric flow measurement has evolved significantly since the early rudimentary methods. Currently, we have technologies such as:

Electromagnetic flowmeters, ideal for conductive fluids such as drinking water. These flowmeters are very cost-effective and their accuracy is suitable for most non-fiscal industrial processes, with an accuracy of 0.5% to 1% of the reading.
Ultrasonic transit-time or Doppler systems are very efficient due to their portability and, above all, the ability to measure flow non-intrusively. However, if they are poorly configured or not properly installed, their accuracy can drop significantly, with an accuracy of 1% to 2% of the reading.
Coriolis mass flowmeters for high-precision applications, widely used in custody transfer (fiscal measurement), can achieve an accuracy of up to 0.025% of the reading. Their biggest disadvantage is their price.

However, these are not the only technologies, as there are some older ones and others that have emerged that have very specific applications, either due to design or industrial culture. For example, for steam measurement, the vortex meter is the most widely used; for natural gas measurement, orifice plate flow measurement is used (differential pressure principle); for liquid petroleum measurement, it is still common to see measurements with positive displacement equipment. This does not mean that there is no other better measurement technology, but rather that the industry seeks the best cost-benefit ratio in measurement.

These principles apply not only to flow measurement in pressurized pipes, but also to free surface or open channel flow measurement. Flow measurement in rivers, canals, weirs, and drainage systems presents unique challenges for measurement and control. Unlike flow in pressurized pipes, where flow rate can be calculated directly, in these systems, the irregular behavior of the fluid (affected by slopes, bed roughness, and atmospheric conditions) makes the energetic approach more practical than the volumetric approach.

In free surface systems, the fluid (usually water) is in contact with the atmosphere, and its movement depends on:

Gravity: The main driving force.
Channel geometry: Slope, cross-section, and roughness.
External conditions: Precipitation, evaporation, and lateral inflows.

These factors generate non-uniform or unsteady behavior, also called transient behavior:

If the flow depth (y) does not change along the channel (with respect to distance x): it is uniform.

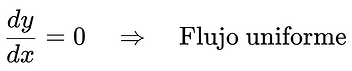
If the flow depth (y) does change along the channel:

If the flow depth (y) does not change with time (t):

If the flow depth (y) does change over time:

However, these changes in depth are not the only associated phenomena. The analysis of these behaviors involves a combination of velocities, which are the Lagrangian velocity (dynamics), the Seddon velocity (kinematics), and the average axial velocity. Normally, the single velocity measured is the average axial velocity. However, both velocities also affect behavior.

Celerities are the speeds at which disturbances (waves) travel in water. Imagine throwing a stone into a river: the waves that form move at a specific velocity, which depends on how the water flows.

1. Lagrangian velocity (dynamics) → Fast waves (like those of a stone). When you throw a stone into a calm river, circular waves form and expand. The speed of these waves is the Lagrangian velocity.

2. Seddon's Velocity (kinematics) → Slow waves (like those of a flood). Now imagine there is a flood in the river. The water rises slowly (it is not an instantaneous wave like that of a stone). This flood wave travels at Seddon's Velocity.

Because it is easier to analyze the flow of a river or channel as a form of energy, it is possible to calculate the flow rate without having to measure the average axial velocity or use the continuity formula (Castelli). This can be done through Manning's formula. However, this is usually used as an approximation because it assumes a uniform flow (which is not always the case) and because it requires knowing very specific parameters such as the roughness of the material and the slope of the channel.

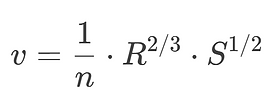
Donde:

v = Velocidad media del agua (m/s).
n = Coeficiente de rugosidad de Manning (adimensional).
R = Radio hidráulico (m), calculado como:
S = Pendiente longitudinal del canal (adimensional)

para calcular el radio hidráulico (R) se utiliza esta fórmula:

A = Wetted cross-sectional area (m²).
P = Wetted perimeter (m).

Flow is a magnitude present, from the veins in your body to the large reservoirs that carry water to cities. Its study and behavior are complex but important for all aspects of life. Making the correct conversions is crucial to understanding the world around us.

If you're interested in learning more about this topic, visit our articles where we explain this and many other topics in more detail.

GO TO CONVERTERS...