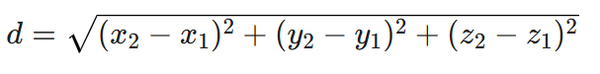Calculadora de Distancias entre Coordenadas 3D |  XYZ

Alguna vez te has preguntado cómo un GPS sabe exactamente dónde estás, o cómo los ingenieros diseñan estructuras complejas con una precisión milimétrica? La respuesta se encuentra en un concepto matemático fundamental: las coordenadas.

​

Nuestra Calculadora de Distancias es una herramienta poderosa que utiliza este sistema para medir el espacio entre múltiples puntos en un entorno tridimensional. Pero para sacarle el máximo provecho, es útil entender qué son exactamente esas coordenadas (X, Y, Z) que estás introduciendo.

​

¿Qué Son las Coordenadas Cartesianas (X, Y, Z)?

​

Imagina que quieres darle a un amigo la ubicación de un tesoro en una habitación vacía. No basta con decirle "está por ahí". Necesitas un sistema de referencia.

Las coordenadas cartesianas son precisamente eso: un "mapa" universal para definir la posición exacta de cualquier punto en el espacio. En un mundo tridimensional como el nuestro, este mapa se compone de tres ejes:

1. Eje X (Derecha - Izquierda): Piensa en este eje como moverte horizontalmente. Es el primer número de tu coordenada y te dice cuántos pasos dar hacia la derecha (si es positivo) o hacia la izquierda (si es negativo) desde un punto de origen (el punto 0).

2. Eje Y (Adelante - Atrás): Este es el segundo número. Una vez que te has movido en el eje X, el eje Y te indica cuántos pasos dar hacia adelante (positivo) o hacia atrás (negativo). Con X e Y, ya puedes ubicar cualquier punto en un plano, como en un mapa tradicional.

3. Eje Z (Arriba - Abajo): Aquí es donde entramos en la tercera dimensión. El eje Z es el tercer número y representa la altura. Te dice cuántos pasos dar hacia arriba (positivo) o hacia abajo (negativo).

​

Al combinar estos tres ejes, (X, Y, Z), puedes describir la ubicación precisa de cualquier objeto en el espacio. Por ejemplo, el punto (4, 5, 3) significa: "desde el origen, muévete 4 unidades a la derecha, 5 unidades hacia adelante y 3 unidades hacia arriba". 

​

Coordenadas Cartesianas vs. Geográficas: Una diferencia clave

​

Es muy importante entender que las coordenadas (X, Y, Z) que utiliza nuestra calculadora son cartesianas. Funcionan perfectamente para medir distancias en espacios definidos y relativamente pequeños, como un sitio de construcción, el diseño de una pieza mecánica o un modelo 3D.

Sin embargo, estas coordenadas no son lo mismo que las coordenadas geográficas (latitud y longitud) que usa un GPS.

• Coordenadas Geográficas (Latitud, Longitud): Son un sistema de coordenadas esféricas diseñado para localizar puntos sobre la superficie curva de la Tierra. Se miden en grados, no en metros o pies.

• Coordenadas Cartesianas (X, Y, Z): Asumen un espacio plano. Intentar usar estas coordenadas para medir grandes distancias sobre la Tierra (como entre dos ciudades) daría un resultado incorrecto, ya que no tienen en cuenta la curvatura del planeta.

​

En resumen: Utiliza nuestra calculadora para proyectos de ingeniería, topografía, diseño o cualquier sistema donde puedas establecer un punto de origen local, para calcular distancias geográficas basadas en latitud y longitud, se requieren fórmulas diferentes y más complejas (como la fórmula de Haversine).

 

¿Cómo Calcula la Distancia Nuestra Herramienta?

​

Cuando introduces dos o más puntos en nuestra calculadora, lo que esta hace es aplicar una extensión del famoso Teorema de Pitágoras al espacio tridimensional.

En la escuela aprendimos que para un triángulo rectángulo, a² + b² = c², nuestra calculadora hace algo similar, pero con las tres dimensiones, para encontrar la distancia en línea recta (la ruta más corta posible) entre cada par de puntos consecutivos, luego, suma estas distancias para darte la longitud total del recorrido.

​

El gráfico 3D que se genera te permite visualizar esta ruta en el espacio, dándote una perspectiva intuitiva de la trayectoria y la posición de tus puntos, especialmente útil para coordenadas obtenidas con estaciones totales.

​