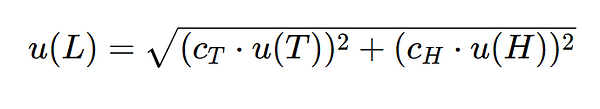La incertidumbre es un parámetro que siempre debe acompañar una medición de cualquier magnitud, ya que ninguna medición esta completa sin su incertidumbre asociada, como siempre existen muchas definiciones y todas son caras de la misma realidad, entonces empecemos por lo primero. Existe un documento llamado GUM (Guide to the expression of Uncertainty in Measurement) que en muchos países se ha vuelto un estándar o norma, por ejemplo en México es la norma NMX-CH-140-IMNC y es el documento que pone las reglas y definiciones de como se debe calcular y expresar dicha incertidumbre.
La explicación formal que viene dada en dicha guía (GUM) define la incertidumbre de medida como un "parámetro asociado con el resultado de una medición, que caracteriza la dispersión de los valores que podrían atribuirse razonablemente al mensurando". En otras palabras, la incertidumbre representa el rango de valores en el cual es probable que se encuentre el valor real de lo que se está midiendo.
Esta definición conlleva otro termino que en ocasiones es poco conocido, "Mensurando". El mensurando es el nombre técnico que usamos en metrología para referirnos a la cantidad específica que queremos medir. Es el objetivo de nuestra medición, el 'qué' estamos tratando de cuantificar. para poner un ejemplo, Si queremos calibrar una báscula, entonces la magnitud es Masa, pero el mensurando es el Error de indicación de dicha báscula, en el caso de un termómetro de líquido en vidrio, la magnitud es temperatura pero el mensurando es la corrección reducida (CR) y un último ejemplo, si tenemos un flujometro, la magnitud es flujo pero el mensurando es el factor del medidor (FM).
Entonces volviendo a la incertidumbre, este parámetro no indica error, sino que expresa la duda razonable sobre el valor medido, teniendo en cuenta los posibles factores de variación en el proceso de medición, estos factores pueden ser tanto intrínsecos al equipo como ambientales y del personal que lleva a cabo la calibración.
En términos mas simples:
Cada vez que hacemos una medición, no importa lo preciso que sea el equipo o cuán cuidadosos seamos, siempre existe un margen de duda. Esa es la incertidumbre. No significa que hayamos hecho algo mal o que el equipo esté dañado simplemente, en el mundo real, las condiciones nunca son 100% perfectas.
La incertidumbre nos ayuda a cuantificar esta realidad. Nos dice que nuestro resultado está cerca del valor verdadero, pero dentro de un rango posible y también se puede interpretar como que es una medición cuantitativa de la calidad de la medición, mientras mas baja sea esa incertidumbre, de mayor calidad es esta medición.
Ahora, es importante saber que existen varios tipos de incertidumbre y se pueden dividir en:
Incertidumbre Tipo A
La incertidumbre de tipo A es la que se evalúa mediante métodos estadísticos. Imagina que hacemos la misma medición muchas veces, con el mismo instrumento, en las mismas condiciones, cada vez, los resultados pueden variar un poco, y esos pequeños cambios se deben a variaciones aleatorias naturales en el proceso de medición. Para cuantificar esta incertidumbre, analizamos esos datos mediante estadísticas (por ejemplo, calculando la media y la desviación estándar).
Cuando se habla de incertidumbre tipo A, te estás basando en datos observados repetidamente, al analizar los resultados, puedes ver cuánto varían y usar esa información para estimar un margen de incertidumbre, cuantas más veces repitas la medición, más precisos serán los datos que tienes sobre esas variaciones. Esta evaluación es confiable porque está basada directamente en observaciones prácticas.
En resumen, la incertidumbre tipo A refleja la variabilidad que se puede observar y cuantificar con métodos estadísticos a partir de datos repetidos.
Incertidumbre Tipo B
La incertidumbre de tipo B es diferente porque no se evalúa a través de mediciones repetidas, sino mediante otro tipo de información. Aqui se debe consider factores como la experiencia previa, la información proporcionada por el fabricante del instrumento, o datos históricos. Por ejemplo, si tienes una balanza y el fabricante especifica que tiene un margen de error de ±0.1 gramos, usas ese dato como una fuente de incertidumbre tipo B.
También puedes considerar la influencia de factores externos que no puedes observar directamente en el momento de la medición, como condiciones ambientales estimadas o limitaciones conocidas del equipo. La incertidumbre tipo B es una combinación de juicio experto, especificaciones y referencias, y aunque no se basa en datos observados directamente, sigue siendo una estimación válida y bien fundamentada.
En resumen, la incertidumbre tipo B es aquella que estimamos basándonos en información externa y experiencia, sin necesidad de realizar mediciones repetidas.
ahora, lo anterior es como se clasifica la incertidumbre, pero también se le puede dividir de acuerdo en que parte del proceso de incertidumbre se encuentre. Pero empecemos por el principio. Cuando se tiene un certificado de calibración ya sea de un laboratorio o un fabricante, normalmente la incertidumbre ya se expresa con un factor de cobertura k=2 o muy cercano a k=2 (si se consideran los grados efectivos de libertad, que veremos mas adelante).
Simplificando pasos: existen magnitudes que afectan directamente al mensurando, por ejemplo, condiciones ambientales, la misma resolución del equipo, su repetibilidad, deriva, etc. estas se conocen como magnitudes de influencia, y aportan una duda o incertidumbre a la medición, a esta se le conoce como incertidumbre asociada. Posteriormente se deben propagar esas incertidumbres y "sumarlas" mediante la ley de propagación de incertidumbre. y así se obtiene la incertidumbre combinada y finalmente se expande con un factor de cobertura de 2 o dos sigma, para asegurar una confianza de aproximadamente el 95%, y así obtenemos la incertidumbre expandida.
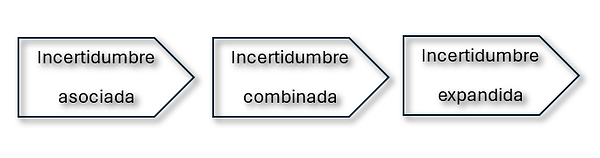
Vamos a explicar un poco a detalle cada tipo de incertidumbre:
Incertidumbre Asociada
La incertidumbre asociada es la incertidumbre de cada componente o magnitud de de influencia que puede influir en el resultado de una medición. Cuando medimos algo, varios factores pueden introducir pequeñas variaciones, como la precisión del equipo o las condiciones del entorno. Estas pequeñas variaciones se representan mediante distribuciones de probabilidad que reflejan la "forma" en que estas variaciones ocurren en cada componente.
Cada distribución tiene su propio "perfil" que describe cómo es probable que se comporten los valores medidos, y esto afecta el valor de incertidumbre asociado de manera diferente.
¿Por Qué Importa la Distribución?
Cada distribución tiene un método particular para calcular la incertidumbre que se adapta a la naturaleza de los datos y refleja mejor la realidad del proceso de medición. Elegir la distribución correcta ayuda a obtener una estimación precisa y confiable de la incertidumbre, adaptada a cómo se comportan los datos en la práctica.
Seleccionar la distribución correcta es clave para una estimación precisa y confiable de la incertidumbre asociada.
Poniendo un ejemplo, se puede decir que si tenemos una balanza con una resolución de 0.01 g, la incertidumbre asociada a esa resolución será uniforme por lo que se tiene lo siguiente:
Incertidumbre Combinada
La incertidumbre combinada es el resultado de agrupar o combinar las incertidumbres asociadas para obtener una medida total de incertidumbre del proceso de medición. Esto se realiza aplicando métodos estadísticos, como "sumar" las incertidumbres, lo cual es apropiado para incertidumbres independientes.
Aquí se toman todas las incertidumbres asociadas de cada componente o magnitud de influencia y se calcula una incertidumbre total. La combinación se realiza de acuerdo a principios estadísticos para reflejar cómo interactúan las incertidumbres en conjunto.
Ejemplo: Si en una medición de temperatura, además del termómetro, intervienen otros factores como la humedad o la estabilidad de la temperatura ambiente, la incertidumbre combinada será el resultado de "sumar" las incertidumbres asociadas de cada uno de estos factores, la suma no se hace algebraicamente, se hace a través de la ley de propagación de incertidumbres que esta declarada por el BIPM (Bureau international des poids et mesures) en la GUM.
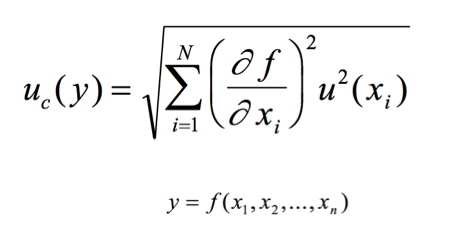
Aquí se entra en otra definición que trae consigo la misma ley de propagación, Los coeficientes de sensibilidad.
Para entender lo que es un coeficiente de sensibilidad (la derivada parcial en la ley de propagación) primero hay que entender que para poder hacer una buena medición o buena calibración, se debe tener el modelo matemático que describe el comportamiento de esa magnitud o mensurando. Ese modelo matemático tiene algunas variables que son magnitudes de influencia, de las que ya hablamos, por ejemplo, la resolución, pero no todas esas variables le afectan al mesurando de la misma manera, algunas tienen mas peso que otras por eso no se pueden simplemente sumar, por lo que es necesario conocer matemáticamente cuanto les afecta, normalmente se mide en porcentaje ya en un presupuesto de incertidumbre y se le conoce como porcentaje de impacto.
El coeficiente de sensibilidad se calcula derivando el efecto de una variable de entrada sobre el resultado de la medición. En general, el coeficiente de sensibilidad (ci) para una variable específica se define como la derivada parcial de la función de medición respecto a esa variable:
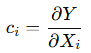
Donde:
Y es el resultado de la medición (mensurando).
Xi es la variable de entrada que influye en Y.
Este valor de ci nos muestra cuánto cambia el resultado (Y) por una pequeña variación en Xi.
Paso a paso para calcular el coeficiente de sensibilidad:
-
Identificar la Función de Medición: Primero, necesitas una fórmula o modelo que relacione el resultado de la medición con las variables de entrada. Por ejemplo, si estás midiendo resistencia eléctrica y sabes que depende de la temperatura, entonces tu modelo incluirá esa relación.
-
Derivar respecto a cada variable de entrada: Calcula la derivada parcial de la función de medición con respecto a cada variable de interés. Esto se hace tomando el modelo matemático y derivándolo con respecto a la variable que quieres analizar. Esto da el coeficiente de sensibilidad ci para esa variable.
-
Evaluar en el Punto de Medición: Si la función incluye constantes o condiciones específicas, como la temperatura ambiente actual o la precisión del instrumento, usa estos valores para evaluar el coeficiente de sensibilidad en esas condiciones.
Ejemplo practico:
Imaginemos que estamos midiendo la longitud (L) de un objeto que depende de la temperatura (T). La relación entre la longitud y la temperatura se expresa mediante la siguiente función:
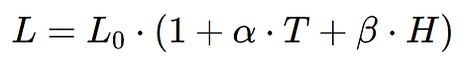
Donde:
-
L0 es la longitud inicial a una temperatura de referencia (por ejemplo, 20 °C).
-
α es el coeficiente de expansión térmica del material.
-
β es el coeficiente de expansión debido a la humedad (cómo afecta la humedad a la longitud del material).
Para encontrar el coeficiente de sensibilidad respecto a la temperatura (cT), derivamos L con respecto a T:
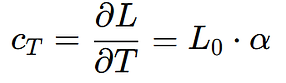
Este resultado nos muestra que el coeficiente de sensibilidad es igual a la longitud inicial multiplicada por el coeficiente de expansión térmica. Esto significa que, por cada grado de cambio en la temperatura, la longitud variará en función de este valor.
Este coeficiente de sensibilidad se usa luego para ajustar la incertidumbre. Si la incertidumbre de la temperatura es, por ejemplo, ±0.5 °C (obtenido de un certificado de calibración), entonces el efecto de esta incertidumbre en la longitud se calcula multiplicando el coeficiente de sensibilidad cT por la incertidumbre de la temperatura. Esto ayuda a determinar cómo la variación en T influye en el resultado de la medición (L). También al multiplicar la incertidumbre de la temperatura que esta en términos de °C por el coeficiente de sensibilidad, lo ayuda a convertir las unidades es términos del mensurando (m).
El otro coeficiente de sensibilidad del modelo matemático sería el siguiente:
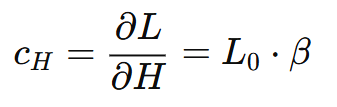
Entonces, teniendo los dos coeficientes del modelo y aplicando la Ley de propagación de incertidumbres, se puede calcular la incertidumbre combinada de la siguiente manera:
Cabe mecionar que u(T) y u(H) pueden propagarse independientemente y puede incluir incertidumbres por certificado, resolución, repetibilidad, deriva, etc.
Incertidumbre Expandida
La incertidumbre expandida es un valor que proporciona un intervalo dentro del cuál se espera que se encuentre el valor real de una medición con un nivel de confianza específico (usualmente 95%). Es una extensión de la incertidumbre combinada uc, que representa solo la incertidumbre estándar en la medición, multiplicada por un factor de cobertura k, que amplía el rango de incertidumbre.
La fórmula general para la incertidumbre expandida U (U mayúscula) es:
U= uc(y)*k
donde k =2.
Para un nivel de confianza de aproximadamente 95%, el factor de cobertura k suele ser 2, aunque este valor puede variar según los grados efectivos de libertad.
Pero ¿que son los grados efectivos de libertad?
Los grados efectivos de libertad (νeff) nos ayudan a determinar el factor de cobertura k cuando las incertidumbres estándar de los componentes de entrada tienen distintos grados de libertad, por ejemplo, en mediciones con diferentes fuentes de incertidumbre o en muestras pequeñas (muestrales). Estos grados de libertad se calculan utilizando el método de Welch-Satterthwaite:
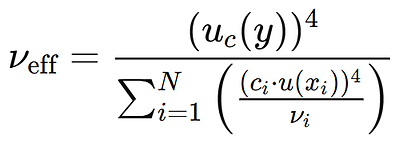
donde:
-
uc(y) es la incertidumbre combinada.
-
ci es el coeficiente de sensibilidad de la variable xi.
-
u(xi) es la incertidumbre estándar de xi.
-
νi son los grados de libertad de cada componente de incertidumbre.
Una vez que se calcula νeff, se utiliza una tabla t de Student para determinar el factor de cobertura k correspondiente al nivel de confianza deseado y a los grados efectivos de libertad.
los grados de libertad ( Vi, diferenciar de grados efectivos de libertad) son asignados para cada componente de incertidumbre en función de la forma en que se ha estimado esa incertidumbre.
Para las incertidumbres evaluadas estadísticamente (Tipo A), los grados de libertad se asignan en función del tamaño de la muestra. En este caso:
-
Si tienes n observaciones de una medición, los grados de libertad son Vi=n−1
-
Esto se debe a que cuando calculamos una desviación estándar a partir de una muestra, perdemos un grado de libertad (porque el cálculo de la media de la muestra usa uno de los datos).
-
Ejemplo: Si tienes 10 mediciones de una longitud y calculas la incertidumbre estándar de la media u(x) de estas mediciones, los grados de libertad asociados serán Vi=10−1=9.
Para las incertidumbres evaluadas por métodos no estadísticos (Tipo B), la asignación de grados de libertad es menos directa. En este caso, el valor se estima en función de la confianza y el conocimiento que tengas sobre la fuente de incertidumbre.
-
Distribución Rectangular (Uniforme): Si la incertidumbre proviene de una fuente con límites conocidos (por ejemplo, un instrumento con precisión declarada de ±EMP), se suele asignar un valor elevado de grados de libertad, ya que se tiene mayor confianza en la exactitud de la estimación (por ejemplo, entre 50 y 100 grados de libertad). Esto depende de la experiencia del metrólogo y el conocimiento en el equipo.
-
Distribución Normal o Gaussiana: Cuando hay suficiente información para asumir que el valor se distribuye normalmente, se puede asignar un valor alto de grados de libertad. Si no tienes datos precisos, un valor común es entre 20 y 30 grados de libertad.
-
Distribución Triangular: Si el valor está más concentrado en torno a un punto (con límites menos definidos), se suele usar un número de grados de libertad intermedio, generalmente entre 10 y 20.
Una ves asignando los grados de libertad y calculando los grados efectivos de libertad por la ecuación de Welch-Satterthwaite, pondremos aplicar la tabla de T-Student, ejemplo:
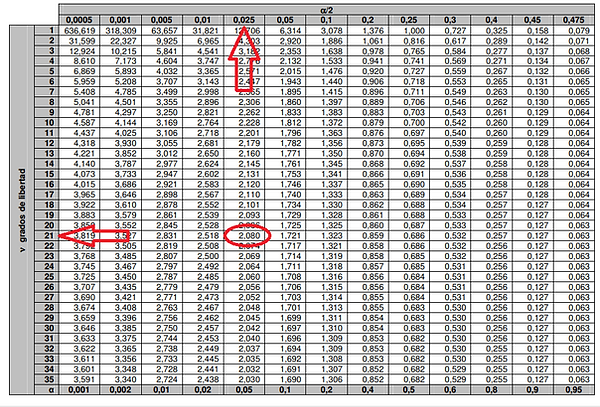
Si en el calculo de Welch-Satterthwaite obtuvimos Veff= 21, osea 21 grados efectivos de libertad, entonces iremos a la Tabla de T-student y buscaremos el valor que corresponde a 21 grados efectivos de libertad y a una confianza del 95% o lo que es lo mismo α/2= 0.025, Entonces nos da un valor k=2.080, para poder multiplicarlo por las incertidumbre combinada y así poder expandirla.
Entonces:
U= uc(y)*k
donde k =2.08.
ahora bien, en la GUM no solo menciona cómo calcular la incertidumbre, sino también como expresarla. la incertidumbre debe expresarse de manera clara y estandarizada para asegurar que los resultados sean comprensibles y útiles, establece varios lineamientos para expresar la incertidumbre de forma que otros usuarios puedan interpretar los resultados de manera consistente.
Ejemplo de una medición de longitud con estos detalles:
-
Resultado: y=10.0 mm
-
Incertidumbre estándar combinada: uc(y)=0.15 mm
-
Factor de Cobertura k=2 (para 95% de confianza)
-
Incertidumbre expandida: U= 0.30 mm
También es válido utilizar el símbolo ± , ejemplo:
10.0 mm ± 0.30 mm
El uso del símbolo ± no se recomienda cuando se usa la incertidumbre estándar o combinada ya que el símbolo se asocia habitualmente con intervalos correspondientes a altos niveles de confianza.
La incertidumbre debe expresarse con dos cifras significativas, a medida de lo posible.
¿Qué Son las Cifras Significativas?
Las cifras significativas son los dígitos en un número que contribuyen a su precisión. En el contexto de incertidumbre, el uso de dos cifras significativas asegura que el valor reportado sea suficiente para entender la variabilidad en la medición sin ser excesivo.
Ejemplo de expresión en dos cifras significativas:
± 0.013578 mm -> ± 0.014 mm
± 0.123456 mm -> ± 0.12 mm
± 123.7 mm -> ± 12 cm
y asi es como en pocas palabras y resumiendo el tema, se calcula la incertidumbre en una medición, entonces ahora ya se puede entender que la acción de solo medir, por si sola, no es suficiente si no se acompaña de el parámetro mas importante dentro de la metrología, y si quieres saber mas sobre metrología, visita nuestro articulo:
